Did you ever finish a bowl of Cheerios and leave a few uneaten o’s floating in the milk? You might have observed how the o’s then congregate together. Ever wonder why? Well, like most things in the physical world, there are mathematical theories to explain why the Cheerios form a clique.
“Liquid likes to lie flat, so what nature does with these particles that are distributed in the liquid is to lump the objects together so the milk can avoid having to crawl up too many things, that minimizes the effort that the liquid has to make,” said Rolf Ryham, Ph.D., associate professor of mathematics at Fordham College at Rose Hill.

Ryham has been working in computational biology for 20 years and he recently received a Fordham Faculty Fellowship to explain these phenomena on a microscopic level. The research will have implications for understanding molecular functions in biology and “the design of novel self-assembling materials,” he said, like the Cheerios in the bowl or, say, oil particles on the surface of water. It can be used when studying proteins in an aqueous cellular environment or in the field of microfluidics, one application of which is separating plasma from other cells in fingerstick blood sampling.
One way to describe the phenomenon of self-assembly in computational biology is through a hybrid approach that Ryham is pioneering. The hybrid employs both a particle-based approach and a continuum approach.
“In the particle-based approach, I can say, ‘I’m going to take my microscope and look deeply into this substance and resolve what these molecules are,’ and in some cases, I don’t necessarily have to resolve the individual molecules, instead I can lump them together and call that a coarse-grained particle.”
A continuum approach is the opposite. In a continuum, mathematicians use differential equations to describe a continuous substance like milk, water, or oil. Liquids have certain physical properties that can be represented by mathematical formulas.
The hybrid that Ryham and his colleagues are working on merges the continuum and the particle-based approaches. To visualize the problem, Ryham returned to his breakfast bowl.
“The particles are the bits of cereal and the continuum is the surface of the milk,” he said. “The interaction is what we’re studying.”
Beyond the Cereal Bowl
Another example beyond the breakfast table would be two boats that are moored next to each other in choppy waters and inevitably drift toward each other until they collide.
“In between the boats the water is not choppy, because the two boats shield that area from the waves,” said Ryham. “Again, nature says, ‘Well I don’t like having this patch of water that’s not choppy. I’m just gonna get rid of it and push these boats together.”
All of biology is a delicate balance between these forces, he said, some of which are understood and some of which are less understood. In the 1960s and 1970s, chemists came to identify the phenomenon as hydrophobic forces.
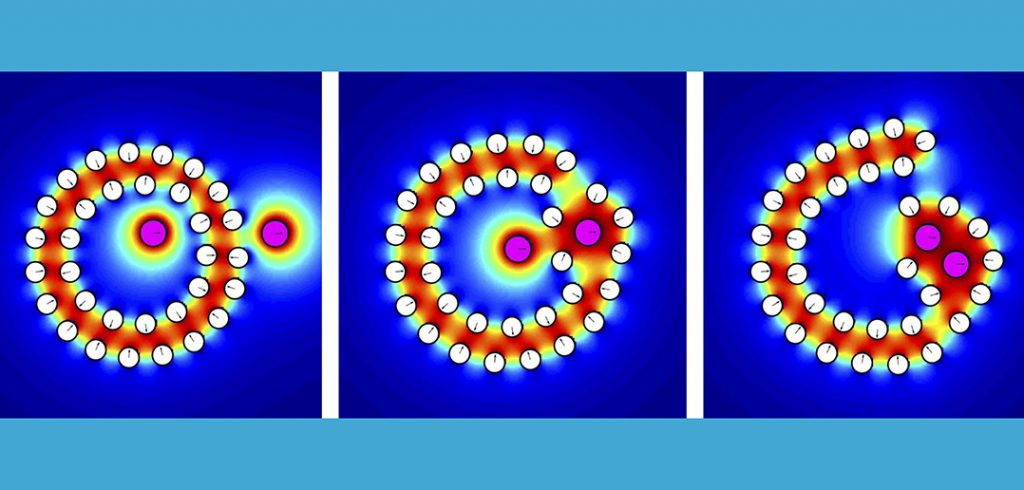
“If you take two hydrophobic substances, like oil on water, you put them together and the oil particles become attracted and come together like the boats in the choppy water,” he said. “The chemists measured this and noted that there was an exponential curve describing the force of attraction. It turns out that the simple representation they came up with could be generalized to objects of arbitrary shapes—like Cheerios. So, we’re trying to calculate that attraction.”
Ryham co-authored a paper with on the subject with Szu-Pei P. Fu, Ph.D., the Peter M. Curran visiting associate professor of mathematics at Fordham. Their article was published this past winter in the journal Multiscale Modeling & Simulation.
A Computational Challenge
In mathematics, these forces of attraction are given voice through “functionals” which are calculated using numerical simulations. Ryham said the computational challenge has been to reduce the time it takes to model a simulation from months to days.
“That’s the thing that keeps up at night, when is this simulation going to finish? How can we make it faster? Then it becomes a question of algorithms and mathematical shortcuts,” he said. “If you’re studying 10 particles it will take one hour to compute, a hundred particles take 10 hours, a thousand particles take a hundred hours.”
One of the mathematical shortcuts the group is using is called an “integral equation method” that allows the simulations to be completed much more quickly.
It’s akin to having many computers simultaneously working on the same problem at the same time through the use of parallel computing or using several graphics processing units. This could potentially turn that one hour into one minute enabling much shorter simulations times, he said.
Merging Science and Math
Ryham said biologists understand the computational challenge but don’t they necessarily want to take it on. Similarly, mathematicians don’t always know what the units in their simulations represent. Ryham’s interests, however, lie somewhere in between.
“You have to be a little bit diplomatic when you go between those two spheres,” he said.
He first became attracted to the sweet spot where math meets science when he worked with a group of physiologists on a problem called membrane fusion.
“These were people who understand the biology and the mathematical language and so we could talk to each other and they gave me a huge appreciation for the complexity of biology,” he said.
The physiologists opened his eyes to modeling challenges in biology that he had trained for as a mathematician.
“It’s the first time that I saw, ‘OK, so I’ve learned all these computational techniques, here is actually a testing ground where we can see how our methods work out,” he recalled.
He noted that computational methods are being developed all the time. But the mathematicians, like many academic communities, can be insularly focused on problems in their discipline.
“That’s not a critical statement if you want to be an expert in something you really have to focus—and maybe that’s the right approach—but I like to see other things as well.”